A Lesson On Heaps Working with FHeaps

The day I found Mary Rose Cook’s blog, I was fascinated! This was exactly the no nonsense virtual mentor I was looking for. A look through her projects is enough to intimidate faint hearted people like me. With great determination, I picked up Fibonacci Heaps as my next project.

The only connection I felt to the topic when I read her post was that I knew what Binary Heaps were, or at least had a reasonable confidence of finding and understanding them quickly and I knew Djikstra’s shortest path algorithm of course. With those as my foundations, I hunted for my DataStructures text book and quickly brushed up on binary heaps and how to create and sort them. Teaching my brother and discussing it with him got me up to speed on it’s space and time complexities. Okay, that was relatively easy.

Now what in heaven’s name were Fibonacci Heaps? I had a vague idea of trees growing in fibonacci numbered rank. I started with Wikipedia. A cursory glance did not help a lot. This was tougher. Mary’s article, of course just whooshed above my head. So, I thought I should start with some basics.

Jonathan Shewchuk’s lecture served as a lengthy but solid starting point. I now knew what priority queues were.Next I looked for some lecture specific to Fibonacci heaps and found this entertaining video. It was somewhat informative but not very convincing in it’s examples. So I decided to tackle it at the source and downloaded Fredman and Tarjan’s paper. The clarity of the paper was very refreshing. It took me two days to absorb it, but by then I could mentally imagine all the operations in the F-Heap.

I am not sure how well I could explain it, but here are my example operations using FHeaps for consideration.

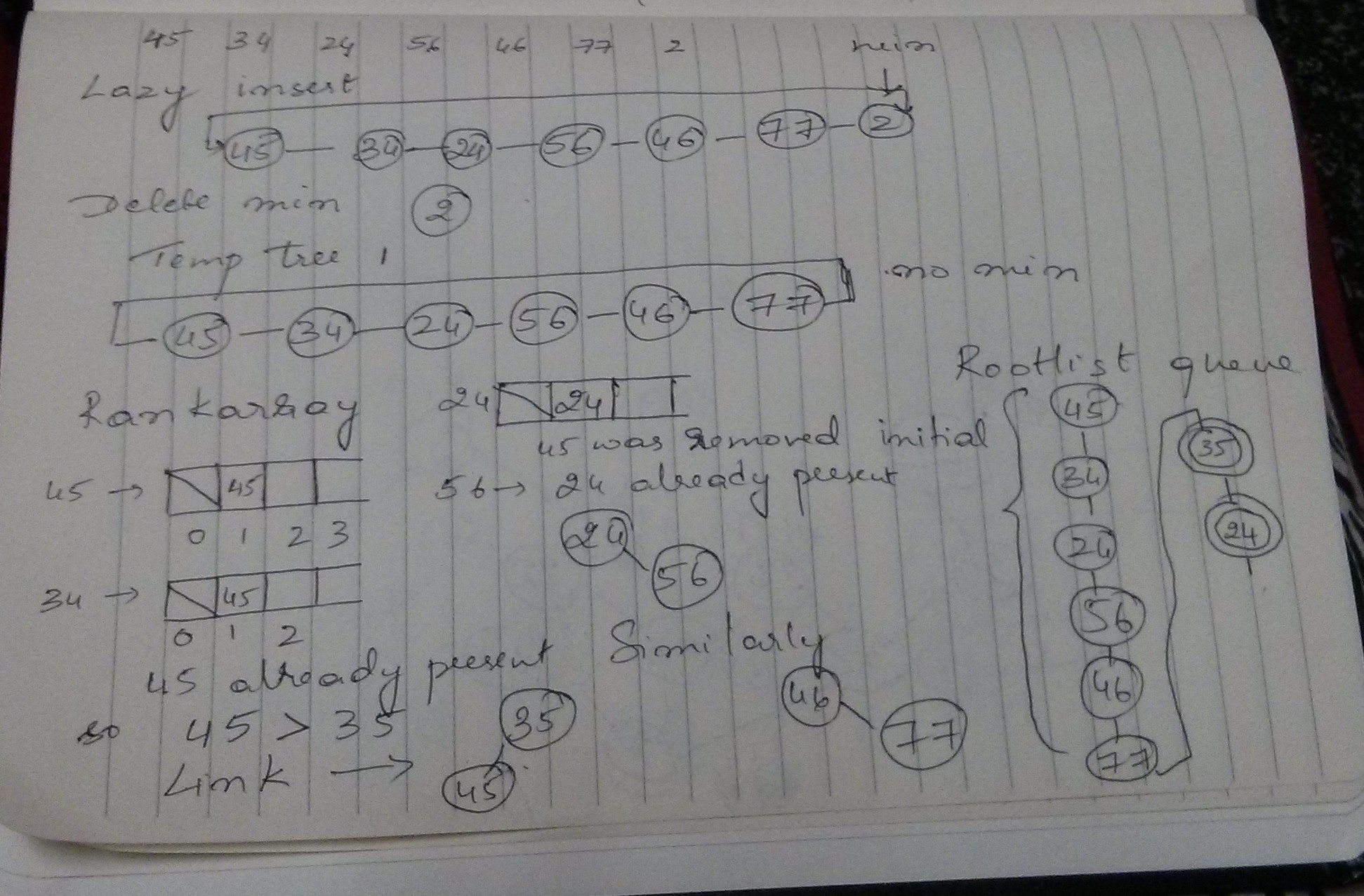
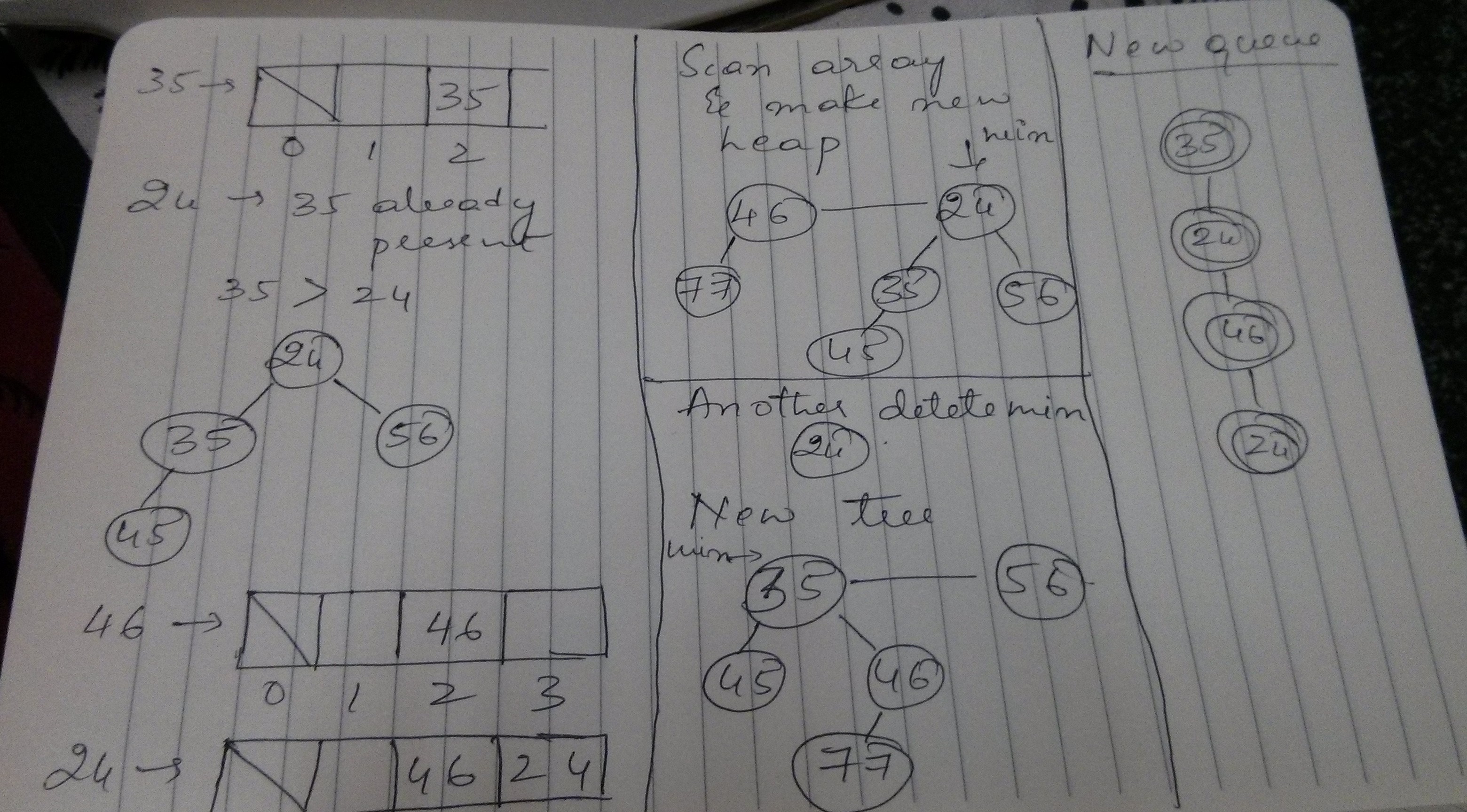
FHeaps are priority heaps whose job is to always give you the smallest key in your heap. The running times for finding minimum are very low because of thier structure. They are thus used in shortest path algorithms and are the best example of speeding an algorithm considerably by only changing datastructure.They achieve this speed by lazy insertion of elements and not sorting the entire heap for every deletion of minimum key.
Having said that, FHeaps mainly perform the following three operations 1. Insert 2. FindMin 3. DeleteMin

I have learnt the decreasemin operation but I havent used it till now, so I will rest my judgement on it’s importance.

Implementation of an FHeap is made using a doubly linked circular list with pointers to parent and child added. A pointer to the minimum node is always maintained in the heap instance and updated after every operation. Hence and FHeap node will look like this.

	Node {
		data,
		next,
		prev,
		parent,
		child,
		rank
	}

1. Insert - During insertion, the new node is lazily added to the list of roots.The pseudocode would be -

	item = new Node(data)
	next = min.next
	next.prev = item;
	item.next = next;
	min.next = item;
	item.prev = min;
	if(item.data < min.data){
		min = item;
	}

1. FindMin -

	
	return min

1. DeleteMin - This is a more complex procedure.

    RemoveMin and make its children part of the root list.
    Iterate through the rootlist and create new heaps by linking the roots which have same rank.
    Do the above until no two trees in the heap have the same rank.
    Now create a new heap out of the new set of trees.
    Compare the roots of the heap and set min to the smallest key.
   

A detailed example is present in the pictures and my implementation in Javascript might help in better understanding.

For an explanation on the outrageous title, I started on this implementation with utmost confidence, but the power of trees and my lack of practice in recursion brought me down comprehensively. I was literally thinking of little numbers inside circles connected to each other for the past two weeks on and off until I finally after two massive attempts at deletemin completed the implementation! And also, I had a grand scheme of showing off my FHeaps using raphael which is still in the works :(

Published